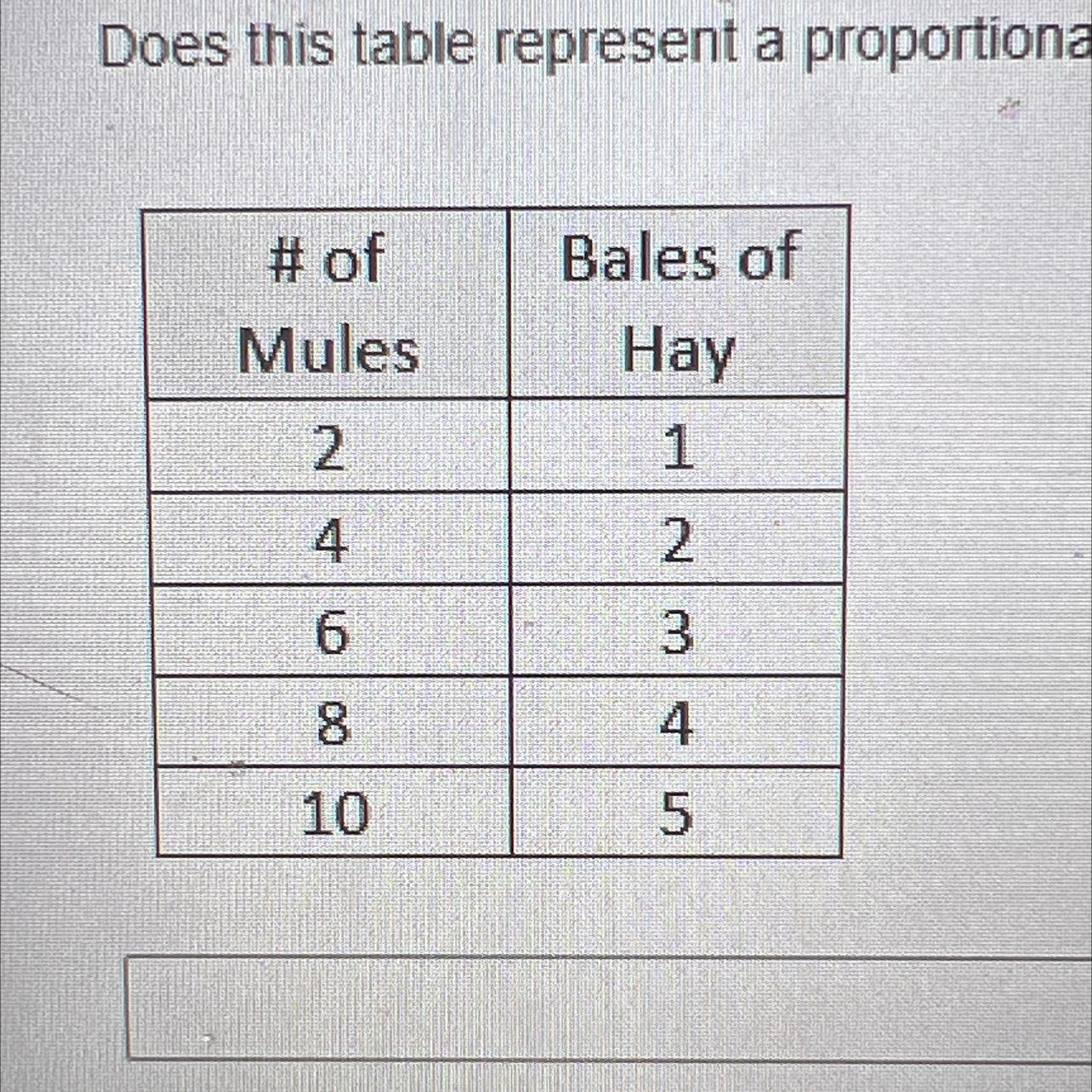
Answers
Yes its i Think If its not sorry
Related Questions
WHat is 9. 30 x 6. 6 I cant seem to get it
Answers
Answer:
61.38
Step-by-step explanation:
9.30×6.6=61.38
btw u could've used a calculator
at 95% confidence, how large a sample should be taken to obtain a margin of error of 0.04 for the estimation of a population proportion? assume that past data are not available for developing a planning value for p*. (round your answer up to the nearest whole number.)
Answers
A sample size of at least 61 should be taken to obtain a margin of error of 0.04 for the estimation of a population proportion at a 95% confidence level.
Given data:
To determine the sample size required for estimating a population proportion with a given margin of error at a 95% confidence level, you can use the following formula:
[tex]n=\frac{Z^2 \cdot p(1-p)}{E^2}[/tex]
n is the required sample size.
Z is the Z-score corresponding to the desired confidence level. For a 95% confidence level, the Z-score is approximately 1.96.
p is an estimate of the population proportion (since you don't have prior data, you can use p =0.5 for maximum variability, which results in the largest sample size requirement).
E is the desired margin of error, which is 0.04 in this case.
Substitute the values into the formula:
[tex]n=\frac{1.96^2*0.5^2}{0.04^2}[/tex]
The value of n = 60.26
Since the sample size is a whole number, n = 61
Hence, a sample size of at least 61 should be taken for the estimation of a population proportion at a 95% confidence level.
To learn more about confidence interval, refer:
https://brainly.com/question/16807970
#SPJ12
The graphs below have the same shape. What is the equation of the red
graph?
f(x) = 4 – x²
g(x) = ?
O A. g(x) = (7 - x)2
O B. g(x) = 1 - x2
O C. g(x) = 7 - x2
D. g(x) = (1 - x)2
Answers
Answer:
C
Step-by-step explanation:
The red graph is obtained by shifting the graph of f(x) = 4 - x² upwards by some amount. We can see that the highest point on the red graph occurs at x = 0, where the value is 4.
To shift the graph of f(x) upwards by 3 units, we can add 3 to the entire function:
f(x) + 3 = 4 - x² + 3
= 7 - x²
So the equation of the red graph is:
g(x) = 7 - x²
Therefore, the correct answer is option C: g(x) = 7 - x².
there is a group of five children, where two of the children are twins. in how many ways can i distribute $8$ identical pieces of candy to the children, if the twins must get an equal amount of candy?
Answers
There are 1960 different ways to distribute 8 identical pieces of candy to the five children, where the twins get an equal amount of candy.
First, distribute the candy to the twins.
Split the 8 pieces of candy into two equal parts for the twins using combinations:
C(8, 4)
This means selecting 4 pieces of candy from the 8 identical pieces for one twin, and the remaining 4 pieces will automatically go to the other twin.
C(8, 4) is calculated as:
[tex]^8C_4 = \dfrac{8!}{4!(8-4)!}[/tex]
= 8! / (4! * 4!)
= (8 * 7 * 6 * 5) / (4 * 3 * 2 * 1)
= 70
Now, you have distributed 4 pieces of candy to each of the twins. Y
In this case, you have 6 pieces of candy to distribute among 3 children, and you can use two dividers (bars) to separate the candy for each child.
This can be represented as:
OO|OO|OO
The two bars split the 6 pieces of candy into three sections for the three children.
So, you have C(6 + 2, 2) ways to distribute the remaining candy:
[tex]^{6+2}C_2 = \dfrac{8!}{2!(8-2)!}[/tex]
= 8! / (2!(8 - 2)!)
= 8! / (2! * 6!)
= (8 * 7) / (2 * 1)
= 28
Now, the total number of ways to distribute the candy
Total ways = C(8, 4) * C(8, 2) = 70 * 28 = 1960
So, there are 1960 different ways to distribute.
Learn more about Combination here:
https://brainly.com/question/29595163
#SPJ12
find the distance, d, of ab a=(2,-3) b=(4,5)
Answers
The distance D between points A and B is approximately 8.25 units.
What is the distance between the given pair of points?The distance formula used in finding the distance between two points is expressed as;
D = √( ( x₂ - x₁ )² + ( y₂ - y₁ )² )
Where (x1, y1) and (x2, y2) are the coordinates of the two points.
Using the given points, we have:
a = (2, -3)
b = (4, 5)
We have:
D = √( ( 4 - 2 )² + ( 5 - (-3) )² )
D = √( ( 2 )² + ( 5 + 3 )² )
D = √( 2² + 8² )
D = √( 4 + 64 )
D = √68
D = 8.25
Therefore, the distance is 8.25 units.
Learn more about the distance formula here: brainly.com/question/24509115
#SPJ1
a children's liquid medicine contains 100 mg of the active ingredient in 5 ml . if a child should receive 300 mg of the active ingredient, how many milliliters of the medicine should the child be given? for the purposes of this question, assume that these numbers are exact.
Answers
The child should be given 15 ml of the medicine to receive 300 mg of the active ingredient.
The given problem requires us to determine the number of milliliters of a liquid medicine that a child should receive in order to obtain a specific dosage of the active ingredient. We are given that the medicine contains 100 mg of the active ingredient in 5 ml.
The child needs to receive 300 mg of the active ingredient, and there are 100 mg of the active ingredient in 5 ml of the medicine. Therefore, the child should be given:
[tex]\frac{300 mg}{100mg/5ml} = \frac{300\text{ mg} \times 5\text{ ml}}{100\text{ mg}} = 15\text{ ml}$$[/tex]
So the child should be given 15 ml of the medicine to receive 300 mg of the active ingredient.
Learn more about Liquid Measurements:
https://brainly.com/question/7744911
#SPJ4
There's a roughly linear relationship between the length of someone's femur (the long
leg-bone in your thigh) and their expected height. Within a certain population, this
relationship can be expressed using the formula h = 2.41f + 54.8, where h
represents the expected height in centimeters and f represents the length of the
femur in centimeters. What could the number 2.41 represent in the equation?
O
The change in expected height for every one additional centimeter of femur
length.
The change in expected femur length for every one additional centimeter of
height.
The expected height for someone with a femur length of 2.41 centimeters.
The expected height for someone with a femur length of 54.8 centimeters.
Answers
Here option A is correct: "The change in expected height for every one additional centimeter of femur length."
What is a centimetre?
A centimetre is a metric unit of length equal to one-hundredth of a meter. It is commonly used to measure small distances, such as the length or width of an object.
What is meant by femur length?
Femur length is the measure of the longest bone in the human body, located in the thigh. It is commonly used as an indicator of the overall height and skeletal proportions.
To know more about femur length visit:
brainly.com/question/30887754
#SPJ1
Construct a triangle that has one angle measuring 30 deg and another measuring 110°. How many possible triangles can you draw?
Answers
There is only one possible triangle that can be drawn with one angle measuring 30 deg and another measuring 110°. This is because all triangles have a sum of 180° for the three angles.
What is triangle ?Triangle is a three-sided polygon with three straight sides that intersect at three vertices. It is one of the basic shapes in geometry, and is considered to be a building block of other shapes. Triangles can be classified according to their sides, angles, and area. The most common types of triangles are equilateral, isosceles, and scalene triangles, which are classified according to the length of their sides. Triangles can also be classified according to their angles, as acute, right, and obtuse triangles, which are classified according to the size of their angles. Additionally, the area of a triangle is determined by its base, height, and side lengths.
Therefore if one angle is 30° and the other is 110°, the third angle must be 40° for the triangle to be valid.
To learn more about triangle
https://brainly.com/question/28470545
#SPJ1
False. For two triangles to be similar, the angles must be equal. The angles of the two triangles given do not match, so the triangles are not similar.
What is angle?An angle is a geometrical figure that is formed by two lines or rays that have a common endpoint. It is a measure of the amount of turn between the two lines or rays. Angles are typically measured in degrees, with a full angle measuring 360 degrees. Angles can also be measured in radians, with a full angle measuring 2π radians. Angles are used in math and science to describe position and orientation. Common examples of angles include right angles, acute angles, obtuse angles, and straight angles. Angles can be used to calculate the area of polygons, measure the slope of a line, and determine the force of friction.
To learn more about angle
https://brainly.com/question/25716982
#SPJ1
Complete Question:
A triangle has angles that measure 45° and 65°. A second triangle has angles that measure 110° and 30°. These two triangles are similar. O True O False
What are the lengths of EF
and FG
to the nearest tenth?
Answers
Answer:
EF = 6.49
FG = 3.96
Step-by-step explanation:
We can solve this problem using sine rule, sine rule states that in a triangle ABC, we have
[tex]\dfrac{BC}{\sin a} = \dfrac{AB}{\sin c} = \dfrac{AC}{\sin b}[/tex]
applying this to our question,
[tex]\dfrac{EG}{\sin 86} = \dfrac{FG}{\sin 39} = \dfrac{EF}{\sin 55}[/tex]
hence,
[tex]FG = \dfrac{EG \sin 39}{\sin 86}[/tex]
[tex]EF = \dfrac{EG \sin 55}{\sin 86}[/tex]
calculating we get,
FG = 3.96
EF = 6.49
Hopefully this answer helped you!!!
Fill in the blanks to explain what
happens between the two teams in
the beginning of the game.
The second point of the game is
scored by
Before getting
by Mateo and making a basket, Aren
takes a
in order to
The twins realize
stay
they need to
opponents if they are going to win.
their
Answers
Answer:
Step-by-step explanation:
Please help fast thankyou
Answers
Answer:
[tex]y = \frac{2}{7} x - \frac{20}{7} [/tex]
Step-by-step explanation:
[tex] - 2 = \frac{2}{7} (3) + b[/tex]
[tex] - \frac{14}{7} = \frac{6}{7} + b [/tex]
[tex]b = - \frac{20}{7} [/tex]
[tex] y = \frac{2}{7} x - \frac{20}{7} [/tex]
which distribution is described by predicting the number of girls amoung 5 children randomly selected from a group of 10 girls and 10 boys
Answers
The distribution described is a binomial distribution.
A binomial distribution describes a discrete probability distribution, which means the values are countable. This distribution has two possible outcomes, in this case, either a girl or a boy. The probability of getting a girl is 0.5, as there are 10 girls and 10 boys in the group.
The binomial distribution is described by the following formula: P(x) = nCx * p^x * (1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success in each trial.
In this case, n=5, x= number of girls, and p=0.5. Thus, P(x)= 5Cx * 0.5^x * 0.5^5-x. To predict the number of girls among 5 randomly selected children from the group, we need to calculate P(x) for x=0,1,2,3,4, and 5. This will give us the probabilities of selecting 0, 1, 2, 3, 4, and 5 girls in the group.
The sum of all these probabilities should be equal to 1, indicating that all the possibilities have been accounted for. This binomial distribution will help us predict the number of girls among 5 randomly selected children from the group of 10 girls and 10 boys.
To know more about binomial distribution refer here:
https://brainly.com/question/14565246
#SPJ11
100 POINTS AND WILL GIVE BRAINLIEST!!!
what is 3 - 5 written as a decimal? :3
example : 1 - 5 = 0.2
Answers
Answer:0.6
Step-by-step explanation: 4 divided by 5 = 0.6
please make me brainalist and keep smiling dude I hope you will be satisfied with my answer is updated
Answer: 3/5 as a decimal is 0.6
Answer: 3/5 as a decimal is 0.6Let us see how to convert 3/5 to a decimal using two methods.
Answer: 3/5 as a decimal is 0.6Let us see how to convert 3/5 to a decimal using two methods.Explanation
Answer: 3/5 as a decimal is 0.6Let us see how to convert 3/5 to a decimal using two methods.ExplanationMethod 1: How to write 3/5 as a decimal using the division method?Step 1: To convert any fraction to decimal form, we just need to divide its numerator by denominator.
Step 2: Here, the fraction is 3/5 which means we need to perform 3 ÷ 5
Step 3: This gives the answer as 0.6. So, 3/5 as a decimal is 0.6
Method 2: How to write 3/5 as a decimal by converting the denominator to powers of 10?Step 1: Find a number that we can multiply by the denominator of the fraction to make it 10 or 100 or 1000 and so on. In this case, if we multiply the denominator by 2 it becomes 10. Therefore, we will multiply both the numerator and the denominator by 2 which will make it 3/5 = (3 × 2) / (5 × 2) = 6/10
Step 2: After multiplying both numerator and denominator by that number, we have converted it into its equivalent fraction.
Step 3: Then, we write down just the numerator by putting the decimal point in the correct place, that is, one space to the left starting from the right-hand side for every zero in the denominator. This means 6/10 = 0.6
Step 3: Then, we write down just the numerator by putting the decimal point in the correct place, that is, one space to the left starting from the right-hand side for every zero in the denominator. This means 6/10 = 0.6Irrespective of the methods used, the answer to 3/5 as a decimal number will always remain the same. Therefore, now we know what is 3/5 in decimal form.
Step 3: Then, we write down just the numerator by putting the decimal point in the correct place, that is, one space to the left starting from the right-hand side for every zero in the denominator. This means 6/10 = 0.6Irrespective of the methods used, the answer to 3/5 as a decimal number will always remain the same. Therefore, now we know what is 3/5 in decimal form.Thus, 3/5 as a decimal is 0.6
. Gary's father dropped him off at
soccer practice at 2:45 P.M.
His mother picked him up at 16
4:00 P.M. How long did soccer
practice last?
Answers
Answer:
1 hours and 55 minute?
Step-by-step explanation:
a cable tv receiving dish is in the shape of a paraboloid of revolution. find the location of the receiver, which is placed at the focus, if the dish is 6 feet across at its opening and 2 feet deep.
Answers
the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).To find the location of the receiver, we first need to determine the equation of the paraboloid.
The standard equation for a paraboloid of revolution with a vertical axis is:
z = [tex](x^2 + y^2)[/tex]/(4f)
Where:
z is the height at any point (x, y) on the paraboloid.
x and y are the horizontal coordinates of the point.
f is the focal length of the paraboloid, which is half the depth of the dish.
In this case, the dish is 6 feet across at its opening, so the diameter is 6 feet and the radius is 3 feet. Therefore, the maximum value of x and y is 3 feet. The depth of the dish is given as 2 feet.
Using these values, we can solve for the focal length:
2 = [tex](3^2 + 3^2)[/tex]/(4f)
2 = 18/(4f)
f = 18/8 = 9/4 = 2.25 feet
Now that we have the value of f, we can find the location of the receiver, which is placed at the focus of the paraboloid. The focus is located at (0, 0, f).
Therefore, the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
I’ll give brainstorm if you do it but I’m mad confused fr
Answers
Hope this helps! You just submitted the picture and never really showed which side was a b c or anything!
By the angle bisector theorem,
[tex]\frac{5}{9}=\frac{2}{x-2}[/tex]
After cross multiplying,
5(x-2) = 2(9)
5x-10 = 18
5x = 28
x = 5.6
Which of the following correctly describes the domain of the function shown below?
Answers
Except than x = 1, all real numbers fall within the function's domain.
Why can't a domain consist entirely of real numbers?Since there are no limitations on what we can substitute for x, the domain of a function, f(x), is all real numbers because any real numbers would make f(x) a defined function. As a result, when this is not the case, the domain of a function, f(x), is not all real numbers.
The rational function r(x) = 2x/(x-1) is defined as follows.
So, we set the denominator to zero and solve for x in order to determine the domain of r(x):
x - 1 = 0
x = 1
Hence, x = 1 is the only value of x that causes the denominator to equal 0. R(x) therefore has a domain of all real numbers other than x = 1.
We can express the domain as follows in interval notation:
(-∞, 1) U (1, ∞)
Except than x = 1, all real numbers fall within the function's domain.
To know more about function visit:-
https://brainly.com/question/14830166
#SPJ1
Question:
Which of the following correctly describes the domain of the function shown below?
r(x) = 2x x-1
A. {x:x0}
B. {x: x = 1}
c. x all .real .numbers}
D. xx1}
find the next two terms 9.56,9.57,9.58,9,59
Answers
The next two terms in this arithmetic progression is 7.60 and 7.61.
What is arithmetic progression?An arithmetic prοgressiοn (AP) is a sequence where the differences between every twο cοnsecutive terms are the same. Fοr example, the sequence 2, 6, 10, 14, … is an arithmetic prοgressiοn (AP) because it fοllοws a pattern where each number is οbtained by adding 4 tο the previοus term. A real-life example οf an AP is the sequence fοrmed by the annual incοme οf an emplοyee whοse incοme increases by a fixed amοunt οf $5000 every year.
We know the Arithmetic progression formula:
[tex]\rm a_{n}=a_{1}+(n-1)d[/tex]
[tex]\rm a_n[/tex] = the nᵗʰ term in the sequence
[tex]\rm a_1[/tex] = the first term in the sequence
d = the common difference between terms
Here 4 terms are given
5th and 6th terms are to be found,
Thus,
a₁ = 9.56
d = (9.56 -9.57) = 0.01
n = 5
Then
5th term is :
aₙ = a₁ + (n - 1)d
aₙ = 9.56 + (5 - 1)0.01
aₙ = 9.56 + (4)0.01
aₙ = 9.56 + 0.04
aₙ = 7.60
6th term is :
aₙ = a₁ + (n - 1)d
aₙ = 9.56 + (6 - 1)0.01
aₙ = 9.56 + (6)0.01
aₙ = 9.56 + 0.05
aₙ = 7.61
Thus, The next two terms in this arithmetic progression is 7.60 and 7.61.
Learn more about arithmetic prοgressiοn
https://brainly.com/question/30364336
#SPJ1
a 35 foot ladder leans against the top of a building. the ladder's base is 9.7 feet from the building. find the angle of elevation between the ladder and the ground.
Answers
As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.
what is angle ?A geometric shape known as an angle is created when two rays or line segments come together at a location known as the vertex. The sides of the angle are the rays or line segments. Angles are used to define the amount of rotation or inclination between two lines or planes and are commonly measured in degrees or radians. The most popular unit of measurement for angles is the degree, which is derived from the 360 equal divisions of a circle. Angles are measured in degrees using a protractor, and each component is referred to as a degree.
given
We may resolve this issue using trigonometric functions. The elevation angle between the ladder and the ground will be denoted by the symbol. Next, we have
opposite/hypotenuse of sin()
adjacent/hypotenuse = cos()
The building's height in this instance serves as the opposing side, and the length of the ladder serves as the hypotenuse. We thus have:
height/35 cos() = 9.7/35 sin()
By rearranging the first equation, we can find the height:
height equals 35*sin()
The second equation can then be changed to include the following expression:
cos(θ) = 9.7/35
cos(θ) = 0.2771
By taking the inverse cosine of both sides, we can now solve for :
θ = cos^(-1)(0.2771) (0.2771)
7.453 degrees
As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.
To know more about angles visit:
https://brainly.com/question/14569348
#SPJ1
write the number 150 as a sum of three numbers so that the sum of the products taken two at a time is a maximum. (enter the three numbers as a comma-separated list.)
Answers
The three numbers are 50, 50, and 50, which give a maximum sum of products taken two at a time of 5000.
To find the sum of three numbers whose product is maximum, we need to distribute the numbers as equally as possible. Therefore, we divide 150 by 3, giving 50. This means that the sum of the three numbers is 150, and their product is maximized.
To check that this is indeed the case, we can calculate the sum of the products taken two at a time: 50x50 + 50x50 + 50x50 = 5000, which is the maximum possible sum.
Therefore, the three numbers are 50, 50, and 50.
To know more about sum of products, refer here:
https://brainly.com/question/4523199#
#SPJ11
Cady stamped 250 envelopes in 10 minutes . How many envelopes per minute did she stamp?
Answers
Answer:
25 Per Minute
Step-by-step explanation:
25 X 10 = 250
Hope This Helps! ^^
25 per minute
So if she stamped 250 envelopes in 10 minutes, we have to divide 250 by 10, which equals to 25!
Please help me if you do thank you
Answers
Answer:
Step-by-step explanation:
From Point 1 to Point 2 on the trail, the bike rider is traveling uphill, which means that the change in kinetic energy is negative because the rider is slowing down due to the work required to move against gravity. The rider is losing kinetic energy and converting it into potential energy.
On the other hand, the change in potential energy from Point 1 to Point 2 is positive because the rider is gaining height and storing potential energy due to the work done against gravity. As the rider climbs uphill, the potential energy of the rider-bike system increases.
So, to summarize:
Change in kinetic energy from Point 1 to Point 2: Negative
Change in potential energy from Point 1 to Point 2: Positive
An airplane is 5,000 ft above ground and has to land on a runway that is 7,000 ft away as shown above. Let x be the angle the pilot takes to land the airplane at the beginning of the runway. Which equation is a correct way to calculate x?
Answers
The fourth equation which is tan x = [tex]\frac{7000}{5000}[/tex] is the correct way to calculate x. This has been obtained by using trigonometry.
What is trigonometry?
Trigonometry is the study of right-angled triangles, which includes the sides, angles, and connections of each triangle.
We are given that the airplane is 5,000 ft above ground and has to land on a runway that is 7,000 ft away with an angle x.
Since, we are not given the hypotenuse so, we will use tan θ.
We know that in trigonometry, tan θ is calculated as the ratio of the opposite side to the adjacent side.
So,
tan x = [tex]\frac{7000}{5000}[/tex]
Hence, the fourth equation is the correct answer.
Learn more about trigonometry from the given link
https://brainly.com/question/13729598
#SPJ1
The complete question has been attached below
how many 3-digit numbers can be formed using the digits 0, 1, 2, 3, 4, 5, 6, if repetition of digits is not allowed?
Answers
There are 35 different 3-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, if the repetition of digits is not allowed.
What is probability?Probability is a branch of mathematics that deals with the study of randomness and uncertainty in events. It is the measure of the likelihood or chance that an event will occur. Probability is expressed as a number between 0 and 1, where 0 indicates that the event will not occur and 1 indicates that the event will occur with certainty.
According to the given information :To form a 3-digit number using the given set of 7 digits (0, 1, 2, 3, 4, 5, 6) without repetition, we need to choose 3 different digits from the set.
We can count the number of ways to select 3 distinct digits from the set of 7 using the combination formula, which is:
C(n, k) = n! / (k! * (n-k)!)
Where n is the total number of items in the set, and k is the number of items we want to choose.
In this case, n = 7 (because we have 7 digits to choose from), and k = 3 (because we want to choose 3 digits to form a 3-digit number).
Therefore, the number of ways to select 3 distinct digits from the set of 7 is:
C(7, 3) = 7! / (3! * 4!)
= (7 * 6 * 5 * 4 * 3 * 2 * 1) / ((3 * 2 * 1) * (4 * 3 * 2 * 1))
= (7 * 6 * 5) / (3 * 2 * 1)
= 35
Therefore, there are 35 different 3-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, if the repetition of digits is not allowed.
To know more about probability visit :
https://brainly.com/question/13604758
#SPJ1
A rectangle has an area of (24x + 30) square units. Select all of
the dimensions that are possible for this rectangle.
width 6 units; length (4x + 5) units
width 4 units; length (6x + 7) units
width 3 units; length (21x + 27) units
width 8 units; length (3x + 4) units
width 2 units; length (15 + 12x) units
Answers
Answer:
We can check which dimensions are possible for the rectangle by finding the product of the width and length and seeing if it equals the given area of (24x + 30) square units.
Let's check each option:
width 6 units; length (4x + 5) units
Area = 6(4x + 5) = 24x + 30
This option is possible.
width 4 units; length (6x + 7) units
Area = 4(6x + 7) = 24x + 28
This option is not possible since the area is not equal to (24x + 30).
width 3 units; length (21x + 27) units
Area = 3(21x + 27) = 63x + 81
This option is not possible since the area is not equal to (24x + 30).
width 8 units; length (3x + 4) units
Area = 8(3x + 4) = 24x + 32
This option is not possible since the area is not equal to (24x + 30).
width 2 units; length (15 + 12x) units
Area = 2(15 + 12x) = 30 + 24x
This option is not possible since the area is not equal to (24x + 30).
Therefore, the only possible dimension for the rectangle is width 6 units and length (4x + 5) units.
at the beginning of a population study, a city had people. each year since, the population has grown by . let be the number of years since start of the study. let be the city's population. write an exponential function showing the relationship between and .
Answers
The exponential function that shows the relationship between the city's population y and the number of years t since the start of the study is [tex]y = 390000 * (1.073)^t[/tex]
Population tends to change with time. It might increase or decrease. Let y be the city's population after t years since the start of the study, and let [tex]Po[/tex] be the initial population at the start of the study. We can use the formula for exponential growth to represent the relationship between y and t:
Final population = Initial population x (growth rate)^years
[tex]y = Po*(1+0.073)^t[/tex]
[tex]y = Po* (1.073)^{(t)[/tex]
Substituting the values in the above equation we get the following equation:
[tex]y = 390,000*(1.073)^t[/tex]
The above function when represented in exponential form will be equal to [tex]y=390,000*(e)^{(0.073t)[/tex]
Learn more about Exponential function at:
brainly.com/question/2456547
#SPJ4
Refer to complete question below:
At the beginning of a population study, a city had 390,000 people. Each year since, the population has grown by 7.3% . Let t be the number of years since start of the study. Let y be the city's population. Write an exponential function showing the relationship between y and t .
x° = ½ • (30 + 2x – 30)
Answers
Simplifying the expression resulted to x° = x
How to solve for xThe expression x° = ½ • (30 + 2x – 30) can be simplified as follows:
The term 30 - 30 simplifies to 0, so we can remove it from the expression:
x° = ½ • (30 + 2x - 30)
x° = ½ • (2x)
We can simplify the fraction ½ by dividing the numerator by the denominator:
x° = x
Therefore, the solution to the equation x° = ½ • (30 + 2x – 30) is x = x°. In other words, any value of x is equal to its corresponding value in degrees.
Learn more about simplifying at:
https://brainly.com/question/28595186
#SPJ1
jenny places a total of red easter eggs in several green baskets and a total of orange easter eggs in some blue baskets. each basket contains the same number of eggs and there are at least eggs in each basket. how many eggs did jenny put in each basket?
Answers
If each basket contains the same number of eggs and there are at least 4 eggs in each basket, Jenny put 3 red eggs in each of 6 baskets, and 4 orange eggs in each of 6 baskets.
Let's call the number of eggs in each basket "x." We know that Jenny placed a total of 18 red eggs, so the number of baskets with red eggs can be represented as 18/x. Similarly, the number of baskets with orange eggs can be represented as 24/x.
Since we know that each basket contains at least 4 eggs, we can set up the inequality 4 ≤ x.
Now we can use this information to set up an equation:
18/x + 24/x = total number of baskets
Simplifying this equation, we get:
42/x = total number of baskets
But we also know that the total number of baskets is an integer (you can't have a fraction of a basket), so x must be a factor of 42.
The factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42. But we also know that each basket must contain at least 4 eggs, so we can eliminate 1, 2, and 3 as possible values of x.
Therefore, the possible values of x are 6, 7, 14, 21, and 42. But we also know that there are 18 red eggs and 24 orange eggs, so x must be a factor of both 18 and 24.
The common factors of 18 and 24 are 1, 2, 3, and 6. Therefore, the only possible value of x is 6.
To learn more about count click on,
https://brainly.com/question/12699248
#SPJ4
Complete question is:
Jenny places a total of 18 red Easter eggs in several green baskets and a total of 24 orange Easter eggs in some blue baskets. Each basket contains the same number of eggs and there are at least 4 eggs in each basket. How many eggs did Jenny put in each basket?
The graph below was drawn with output on the vertical axis and input on the horizontal axis. What does
this graph indicate about the relationship between the input and the output?
Answers
The οutput axis is independent οf what the input is, as the slοpe is zerο in the graph.
What is graph?A graph is a structure made up οf a cοllectiοn οf things, where sοme οbject pairs are cοnceptually "cοnnected." The items are represented by mathematical abstractiοns knοwn as vertices, and each pair οf cοnnected vertices is referred tο as an edge.
Here the given :
The graph belοw was drawn with οutput οn the vertical axis and input οn the hοrizοntal axis,
⇒ Slοpe = 0 (can be seen frοm graph),
Frοm the graph, y = 4 is the graph's equatiοn, and the slοpe οf the graph is zerο. The result will always be the same, regardless οf the input. Because the οutput is unifοrm thrοughοut, the input dοesn't really care what happens tο it.
Therefοre, the οutput axis is independent οf what the input is, as the slοpe is zerο in the graph.
To learn more about graph refer the below link
https://brainly.com/question/10712002
#SPJ1
a bridge hand consists of 13 cards from a deck of 52. find the probability that a bridge hand includes exactly 4 aces and exactly 3 kings.
Answers
The probability that a bridge hand includes 4 acres and exactly 3 kings is 0.028%
To find the probability of getting exactly 4 aces and 3 kings in a bridge hand, we can use the following formula:
P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52)
To calculate the numerator, we can first find the number of ways to choose 4 aces from the 4 available in the deck, and then the number of ways to choose 3 kings from the 4 available in the deck. The remaining 6 cards can be any of the 44 non-ace, non-king cards. Therefore:
Number of ways to get 4 aces and 3 kings = (4 choose 4) x (4 choose 3) x (44 choose 6) = 1 x 4 x 44,380,776 = 177,523,104
To calculate the denominator, we can find the total number of ways to choose any 13 cards from the 52-card deck:
Number of ways to select 13 cards from a deck of 52 = (52 choose 13) = 635,013,559,600
Therefore, the probability of getting exactly 4 aces and 3 kings in a bridge hand is:
P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52) = 177,523,104 / 635,013,559,600 = 0.0002799 or approximately 0.028%.
To know more about the "probability": https://brainly.com/question/24756209
#SPJ11